مخطط الموضوع
-
-
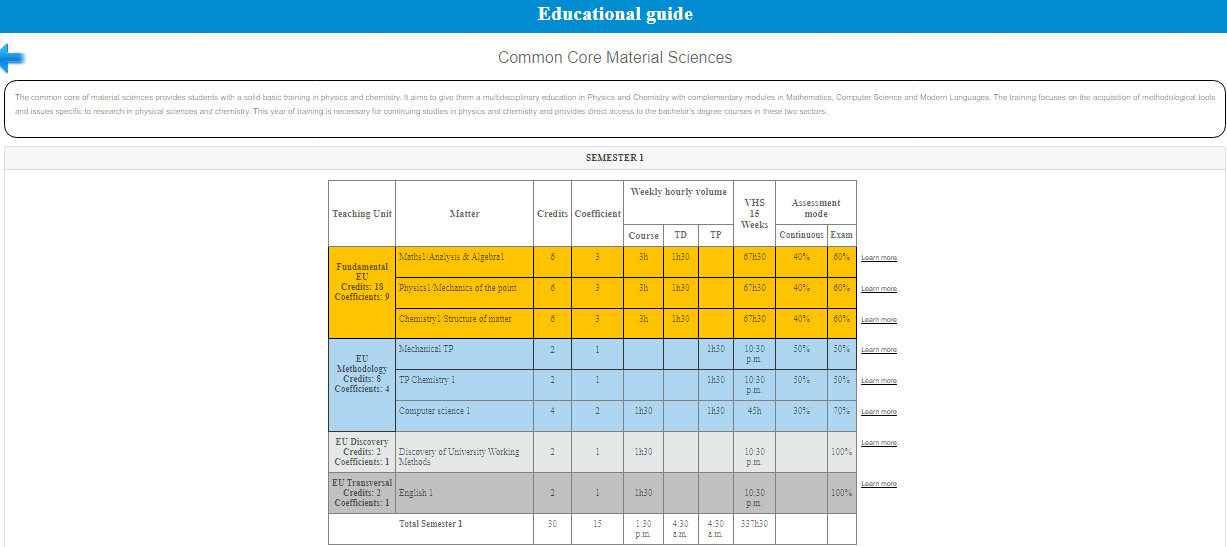
Mathematics 1/ Analysis & Algebra 1
Acquisition of basic mathematical formalisms in Analysis and Algebra and their applications.
Credits: 6
Coefficient: 3
Evaluation method: Continuous: 33% Exam: 67%
-
Opened: الثلاثاء، 7 يناير 2025، 12:00 AMDue: الجمعة، 24 يناير 2025، 11:59 PM
This test is for all students in the class for review.
( هذا الاختبار لجميع طلبة الفصيلة يكون للمراجعة )
-
-
2 Structure of real numbers eld R Dr L.Derbal 22
2.1 Set of rational numbers Q. . . . . . . . . . . . . . . . . . . . . . 22
2.1.1 Integers numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.2 Rational Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2 Irrational Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23
2.3 Real numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.3.1 Axiomatic de nition . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.3.2 Absolute value . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.3.3 Bounded Sets of R . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.3.4 Dense groups in R . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.3.5 Intervals in R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
-
-
-
3 Real Functions of a Real Variable Dr.L. DERBAL 35
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.1.1 Bounded functions, monotonic functions . . . . . . . . . . . . . . . 35
3.1.2 Odd, even, periodic function . . . . . . . . . . . . . . . . . . . . . 36
3.1.3 Algebraic operations on functions . . . . . . . . . . . . . . . . . . . 37
3.1.4 Limit of a function . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.1.5 Limit theorems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.1.6 Operations of Limits . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3.2 Continuity of a function . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.2.1 General de nition . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.2.2 Operations on continuous functions . . . . . . . . . . . . . . . . . . 46
3.2.3 Continuity of composition function . . . . . . . . . . . . . . . . . . 46
3.2.4 The Intermediate Value Theorem . . . . . . . . . . . . . . . . . . . 47
3.2.5 Uniform Continuity . . . . . . . . . . . . . . . . . . . . . . . . . . 48
3.3 Derivable function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.3.1 De nition and properties . . . . . . . . . . . . . . . . . . . . . . . 51
3.3.2 One-sided derivatives . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.3.3 Operations on derivative functions: . . . . . . . . . . . . . . . . . . 53
3.3.4 Derivative of usual functions . . . . . . . . . . . . . . . . . . . . . 56
3.3.5 The nth derivative . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.3.6 Hôspitals Rule: . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
3.4 Elementary functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.4.1 Trigonometric functions . . . . . . . . . . . . . . . . . . . . . . . . 68
3.4.2 Exponential function . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.4.3 Logarithm function . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.4.4 Logarithm function of any base . . . . . . . . . . . . . . . . . . . . 77
3.4.5 Power function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
3.4.6 Hyperbolic functions and their inverses . . . . . . . . . . . . . . . 78
-
-